数据结构与算法之二叉树
摘要
本文讲解了二叉树的基本概念及其链式和顺序存储方式,重点介绍了完全二叉树的特性及其在存储优化中的应用。作者通过图示和代码示例,说明了完全二叉树如何利用数组高效存储和操作节点,展示了其在计算机科学中的重要性和实用性。
什么是二叉树
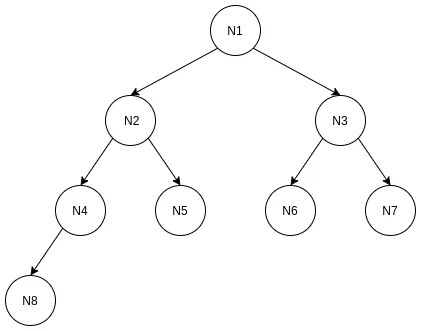
二叉树的知识点, 需要有链表的基础知识, 一般二叉树的结构如图示:
二叉树是一种树状结构.
所谓二叉, 就是一个节点最多可以延伸出两个子节点. 对于二叉树的节点一般会有一些固有称呼. 如上图,
- 一般会把N1节点叫做"根结点“或者”root节点";
- 会把N2叫做N1的"左子节点", N3叫做N1的"右子节点";
- N1则是N2或者N3的"父节点“或者”parent节点";
- N2或者N3可以是N2或者N3子树的根结点, 但是不是N1树的根结点;
- 同理, 对N4或者N5, N2是他们的父节点, N3是他们的"叔叔节点“或者”uncle节点";
- 对于N4, N6或者N7这种在末尾的节点, 叫做"叶子节点";
- 从根结点到叶子节点经历过的最多的节点数叫做"树的深度", 所以N1树的深度是4, 节点N1的深度是1(从上往下);
- 从叶子结点到根节点经历过的最多的节点数叫做"树的层数", 所以N1树的层数是4, 节点N1的层数是4(从下往上);
一般对于普通的二叉树, 我们可以用链表表示, 比如给定一个二叉树节点的结构体类型
| |
如上链表结构的结构体Node, 至少占用24Byte, 而实际数据只有一个int(假设是4Byte), 浪费了较多的空间.
占用24Byte是因为struct会有内存对齐的策略, 比如64位机器上int是4Byte, 但是两个指针是8Byte, 则需要按照8Byte对齐, 所以一共是24Byte
完全二叉树
普通二叉树一般会用链表结构存储, 会多出至少两个成员用来存储其左右孩子节点, 但是有一种比较特殊的二叉树, 可以直接使用顺序结构存储, 不需要存储左右孩子节点的指针; 这就是完全二叉树;
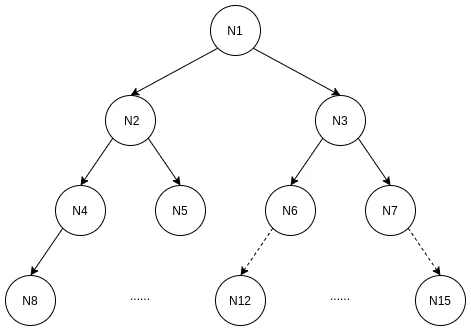
完全二叉树的结构如下图所示,
上面有两种二叉树, 一种是满二叉树, 一种是完全二叉树;
满二叉树是指, 除了叶子节点外, 每个节点有且只有两个只节点; 假设一棵满二叉树的深度为h, 有n个节点, 最大层数为k, 则满足:
- 满二叉树的节点数 n = 2 ^ h - 1;
- 满二叉树第一层的节点树 = 2 * (h - 1);
假设一棵完全二叉树的深度为h, 有n个节点, 最大层数为k, 则满足, 深度为1 ~ h-1的结点构成满二叉树, 深度h的结点都是叶子结点, 如果是右结点, 则必有左结点.
相当于是一个装了球的盒子, 往左倾斜, 则如果有右边的球(结点), 则必有左边的球(结点).
- 完全二叉树的节点数 2 ^ h - 1 >= n >= 2 ^ (h - 1) - 1
- 完全二叉树第一层的节点树 <= 2 * (h - 1);
完全二叉树顺序存储
区别于一般的链式存储, 顺序存储一般会占用更少的内存空间, 而且连续的内存也可以方便硬件加速.
满二叉树
满二叉树可以说是特殊的完全二叉树(其实完全二叉树是通过满二叉树演变过来的).
对于满二叉树, 我们从上往下, 从左往右, 给每个结点从0开始按顺序编号.
对于第k个结点, 可以推算出其左右孩子结点分别是第2*(K + 1) - 1个结点和第2*(K + 1)个结点;
其父结点是第[(k - 1)/2](取整)个结点;
所以, 即使我们把满二叉树的所有结点放在顺序结构, 如数组中, 可以非常方便的遍历每个结点的子结点和父结点.
| |
完全二叉树
方便理解, 可以把完全二叉树补充为满二叉树, 也用顺序结构存储. 对于原本不存在的数据(N9-N15), 用null表示; 这样在遍历的时候, 遇到null则表示没有这个数据;
| |
实际上, 这些null的数据都在数组的末尾, 进一步简化, 可以把这些null数据都去掉, 仅保存完全二叉树中有效的数据.
| |
此时, 在遍历父结点或者子结点是, 只需要判断当前结点的下标或者子结点的下标是否在数组的大小范围内即可;
| |