单调栈
顾名思义, 单调栈就是其元素单调的栈, 满足两个特性:
当然, 关于第二点也可以是单调不递减(>=)或者单调不递增(<=).
构造一个单调栈
从实践出发, 看看怎么构建一个单调栈;
比如有一个正整数列表: [2 1 3 4 7 5]
构建其中之一的单调不递减栈:
- 列表是否空? 如果空则转2, 否则转3;
- 退出;
- 从列表中取出元素, 转4;
- 栈是否空? 如果空则转5, 否则转6;
- 元素入栈, 转1;
- 新元素与栈顶元素比较, 如果满足大小关系, 入栈, 转1; 否则, 出栈, 转4;
按照上述算法, 构建单调栈:
- 新元素比栈顶元素小(1->3->4->6->4->5)
- 新元素比栈顶元素大, 入栈(1->3->4->6)
- 新元素比栈顶元素大, 入栈(1->3->4->6)
- 新元素比栈顶元素大, 入栈(1->3->4->6)
- 新元素比栈顶元素小, 则弹出栈顶元素, 直到新元素比栈顶元素小或者栈空(1->3->4->6->4->5->2)
以上, 已经有几分像是一个状态机, 入栈出栈都是状态的变化.
 单调栈
单调栈
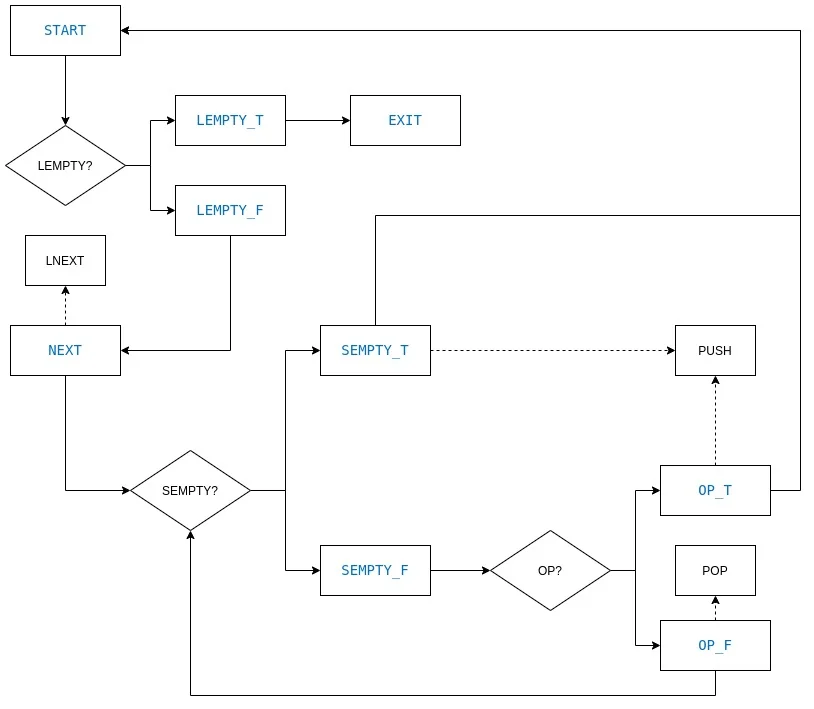
上图是将单调栈转换成状态和操作, 蓝色字体表示状态, 黑色字体表示操作, 实线表示状态转换, 虚线表示附加操作.
下面, 我们不妨尝试使用状态机实现从一个列表生成单调栈的函数.
单调栈的代码实现
首先, 我们定义几个状态, 根据上述的流程图, 有以下几个状态:
开始/下一个/栈空/栈不空/满足大小/不满足大小/列表空/列表不空/退出
1
2
3
4
5
6
7
8
9
10
11
12
| enum class STAT
{
START,
NEXT,
SEMPTY_T,
SEMPTY_F,
OP_T,
OP_F,
LEMPTY_T,
LEMPTY_F,
EXIT
};
|
与状态对应的, 还有一些操作:
判断栈是否空/比较操作/判断队列是否空/从队列中取下一个元素/入栈/出栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| auto sempty = [&]() -> bool {
return s.empty();
};
auto op = [&](const int &a) -> bool {
return fop(s.top(), a);
};
int lpos = 0;
auto lempty = [&]() -> bool {
return lpos >= list.size();
};
auto lnext = [&]() -> int {
return list[lpos++];
};
auto push = [&](const int &a) {
s.push(a);
};
auto pop = [&]() {
s.pop();
};
|
最后就是状态之间的跳转规则, 直接按照流程编写跳转规则就好
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| do
{
switch (stat)
{
case STAT::START:
stat = lempty() ? STAT::LEMPTY_T : STAT::LEMPTY_F;
break;
case STAT::NEXT:
a = lnext();
stat = sempty() ? STAT::SEMPTY_T : STAT::SEMPTY_F;
break;
case STAT::SEMPTY_T:
push(a);
stat = STAT::START;
break;
case STAT::SEMPTY_F:
stat = op(a) ? STAT::OP_T : STAT::OP_F;
break;
case STAT::OP_T:
push(a);
stat = STAT::START;
break;
case STAT::OP_F:
pop();
stat = sempty() ? STAT::SEMPTY_T : STAT::SEMPTY_F;
break;
case STAT::LEMPTY_T:
stat = STAT::EXIT;
break;
case STAT::LEMPTY_F:
stat = STAT::NEXT;
break;
}
} while (STAT::EXIT != stat);
|
下面是完整的代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
| #include <stack>
#include <vector>
#include <iostream>
#include <string>
using namespace std;
enum class STAT
{
START,
NEXT,
SEMPTY_T,
SEMPTY_F,
OP_T,
OP_F,
LEMPTY_T,
LEMPTY_F,
EXIT
};
template <typename FOP>
void mStack(stack<int> &s, const vector<int> &list, FOP &&fop)
{
auto sempty = [&]() -> bool {
return s.empty();
};
auto op = [&](const int &a) -> bool {
return fop(s.top(), a);
};
int lpos = 0;
auto lempty = [&]() -> bool {
return lpos >= list.size();
};
auto lnext = [&]() -> int {
return list[lpos++];
};
auto push = [&](const int &a) {
s.push(a);
};
auto pop = [&]() {
s.pop();
};
STAT stat = STAT::START;
int a = -1;
do
{
switch (stat)
{
case STAT::START:
stat = lempty() ? STAT::LEMPTY_T : STAT::LEMPTY_F;
break;
case STAT::NEXT:
a = lnext();
stat = sempty() ? STAT::SEMPTY_T : STAT::SEMPTY_F;
break;
case STAT::SEMPTY_T:
push(a);
stat = STAT::START;
break;
case STAT::SEMPTY_F:
stat = op(a) ? STAT::OP_T : STAT::OP_F;
break;
case STAT::OP_T:
push(a);
stat = STAT::START;
break;
case STAT::OP_F:
pop();
stat = sempty() ? STAT::SEMPTY_T : STAT::SEMPTY_F;
break;
case STAT::LEMPTY_T:
stat = STAT::EXIT;
break;
case STAT::LEMPTY_F:
stat = STAT::NEXT;
break;
}
} while (STAT::EXIT != stat);
}
int main()
{
vector<int> cs{2, 1, 3, 4, 7, 5};
stack<int> ss;
mStack(ss, cs, [](const int &a, const int &b) { return a < b; });
while (!ss.empty())
{
cout << ss.top() << " ";
ss.pop();
}
return 1;
}
|
聊一两句状态机
要写状态机, 需要明确有几个状态, 和状态的对应操作, 也需要明确状态间的跳转规则;
个人认为, 状态机的代码很容易维护, 只需要关注下一个状态就行了, 需求变更的时候, 改起来非常的方便;
上面的状态机肯定还有很多优化空间的, 但是目前还没打算研究这个专题, 后期会专门系统地看看状态机的编写方法;
每日温度
这是对应leetcode题739.
给一个每天的温度列表, 返回一个列表, 表示至少多少天后的温度比这一天高, 例如输入温度[73, 74, 75, 71, 69, 72, 76, 73], 返回[1, 1, 4, 2, 1, 1, 0, 0]。
这是比较经典的单调栈的例子, “第一个比当前大/小的元素”.
我们可以从后往前构造一个单调递减栈, 栈中元素是温度的下标, 用温度大小做比较;
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| vector<int> dailyTemperatures(vector<int> &T)
{
stack<int> st;
int si = T.size();
vector<int> rd(si);
for (int i = si - 1; i >= 0; i--)
{
while (!st.empty() && T[i] >= T[st.top()])
{
st.pop();
}
if (!st.empty())
{
rd[i] = st.top() - i;
}
else
{
rd[i] = 0;
}
st.push(i);
}
return rd;
}
|