遍历二叉树的作用
基于二叉树的结构, 衍生出了二叉查找树/平衡二叉查找树/堆等等结构或算法(这些之后会讲), 学会如何遍历一颗二叉树是学习此类"派生二叉树"的基础.
二叉树的遍历
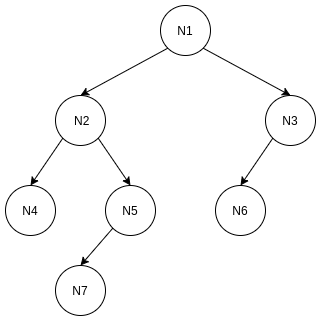
我们先来看一颗一般的二叉树. 然后根据不同的遍历方式, 看看这颗二叉树结点最终遍历的顺序. 二叉树
二叉树
前序遍历
前序遍历就是按照先根结点, 再左右子结点的方式去遍历(root -> left -> right).
对一个链式存储的二叉树来说, 代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
| vector<int> pre;
vector<int> preorderTraversal(TreeNode* root) {
if (!root)
{
return pre;
}
pre.push_back(root->val);
preorderTraversal(root->left);
preorderTraversal(root->right);
return pre;
}
|
我们先跟着代码的逻辑走一遍:
- 操作N1左子结点N2, N2是N2子树的根结点, push进队列
- 操作N2左子结点N4, N4是N4子树的根结点, push进队列
- N4没有子结点, 操作N4的父结点N2的右子结点N5, N5是N5子树的根结点, push进队列
- 操作N5左子结点N7, N7是N7子树的根结点, push进队列
- N7没有子结点, 退回到父结点, 直到发现N1有右子结点N3, N3是N3子树的根结点, push进队列
1
| [N1, N2, N4, N5, N7, N3]
|
- 操作N3左子结点N6, N6是N6子树的根结点, push进队列, 全部遍历完成
1
| [N1, N2, N4, N5, N7, N3, N6]
|
所以, 最终按照前序遍历的结果是:
1
| [N1, N2, N4, N5, N7, N3, N6]
|
使用递归的编程技巧很容易实现前序遍历的代码, 但是递归有太多的临时变量, 随着递归深度的增加, 消耗的内存也在一直增加;
(对二叉树这种结构, 递归还可接受, 递归深度一般是logn, 不过极端情况可以达到n)
如何不使用递归实现前序遍历呢?
非递归方法实现前序遍历
这里, 我参考图遍历中一般会用的两个表, OPEN表和CLOSE表实现二叉树的前序遍历, OPEN表和CLOSE表在图论中会讲到.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| vector<int> preorderTraversal(TreeNode* root) {
vector<int> pre;
if (!root)
{
return pre;
}
stack<TreeNode *> open;
vector<TreeNode *> close;
auto is_visited = [&] (TreeNode * node) -> bool {
for (const auto cn : close)
{
if (cn == node)
{
return true;
}
}
return false;
};
open.push(root);
while(!open.empty())
{
TreeNode *top = open.top();
if (!is_visited(top))
{
close.emplace_back(top);
pre.emplace_back(top->val);
}
if (top->left && !is_visited(top->left))
{
open.push(top->left);
}
else if (top->right && !is_visited(top->right))
{
open.push(top->right);
}
else
{
open.pop();
}
}
return pre;
}
|
open表中存储了待遍历的结点, close表中存储了已经遍历过的结点. 那么上述代码的大致思想是:
- 初始化open表, 将root结点push进表;
- 如果open表的top元素没有被遍历过(不在close)表, 这储存其值, 并将top结点加入到close表;
- 如果open表的top元素的left结点存在且没有被遍历过, 则将left结点push进open表;
- 如果3失败, 但是open表的top元素的right结点存在且没有被遍历过, 则将right结点push进open表;
- 如果3/4都失败, 则说明子结点不存在或者都被遍历过, 则弹出top元素;
中序遍历
中序遍历就是按照先左子结点, 再根结点, 最后右子结点的方式去遍历(left -> root -> right).
1
2
3
4
5
6
7
8
9
10
11
12
13
| vector<int> pre;
vector<int> preorderTraversal(TreeNode* root) {
if (!root)
{
return pre;
}
preorderTraversal(root->left);
pre.push_back(root->val);
preorderTraversal(root->right);
return pre;
}
|
中序遍历可以自行思考遍历的过程, 按照中序遍历的结果是:
1
| [N4, N2, N7, N5, N1, N6, N3]
|
后序遍历
后序遍历就是按照先左右子结点, 再根结点的方式去遍历(left -> right -> root).
1
2
3
4
5
6
7
8
9
10
11
12
13
| vector<int> pre;
vector<int> preorderTraversal(TreeNode* root) {
if (!root)
{
return pre;
}
preorderTraversal(root->left);
preorderTraversal(root->right);
pre.push_back(root->val);
return pre;
}
|
后序遍历可以自行思考遍历的过程, 按照后序遍历的结果是:
1
| [N4, N7, N5, N2, N6, N3, N1]
|
二叉树非递归遍历总结
以leetcode题AC作为验证:
栈
前序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| vector<int> preorderTraversal(TreeNode* root) {
if (root == nullptr)
return {};
vector<int> result;
stack<TreeNode *> st;
st.push(root);
while(!st.empty())
{
TreeNode *node = st.top();
st.pop();
result.emplace_back(node->val);
if (node->right)
st.push(node->right);
if (node->left)
st.push(node->left);
}
return result;
}
|
中序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| vector<int> inorderTraversal(TreeNode* root) {
if (root == nullptr)
return {};
vector<int> result;
stack<TreeNode *> st;
TreeNode *node = root;
while(!st.empty() || node != nullptr)
{
if (node)
{
st.push(node);
node = node->left;
}
else
{
node = st.top();
st.pop();
result.emplace_back(node->val);
node = node->right;
}
}
return result;
}
|
后序遍历
后序遍历中, 任一节点的前驱节点是它的右子节点, 如果右子节点不存在则是左子节点, 这即是lastnode存在的意义.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| vector<int> postorderTraversal(TreeNode* root) {
if (root == nullptr)
return {};
vector<int> result;
stack<TreeNode *> st;
st.push(root);
TreeNode *lastnode = root;
while(!st.empty())
{
TreeNode *node = st.top();
st.pop();
bool is_leaf = (node->left == nullptr) && (node->right == nullptr);
bool is_lastpre = (node->left == lastnode || node->right == lastnode);
if (is_leaf || is_lastpre)
{
result.emplace_back(node->val);
lastnode = node;
}
else
{
st.push(node);
if (node->right)
st.push(node->right);
if (node->left)
st.push(node->left);
}
}
return result;
}
|
morris
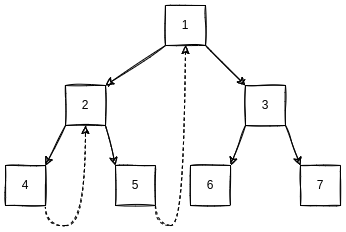
morris的目标是将遍历的空间复杂度降低到O(1), 通过对本文提及的三种遍历方法的认识, 可以理解到, 其难点在于怎么回到"父节点"(这里的父节点相对广义, 也可以是祖父节点之类). 那么, morris的核心思想就是通过利用二叉树叶子节点的空闲指针帮助回到"父节点". 如下:
 morris指针
morris指针
利用左子树的最右侧叶子节点的右指针指向root节点, 在前序遍历和中序遍历的时候, 可以很方便的回到root节点.
比如前序遍历, 先做root节点, 然后做左子树, 左子树做完, 正好通过左子树的最右侧叶子节点的右指针回到了root节点(因为左子树的最右侧叶子节点是左子树最后一个被访问的节点), 此时可以做右子树.
又比如中序遍历, 然后做左子树, 左子树做完, 正好通过左子树的最右侧叶子节点的右指针回到了root节点(因为左子树的最右侧叶子节点是左子树最后一个被访问的节点), 然后做root节点, 接下来又方便的转移到右子树.
但是后序遍历则不这么直观, 因为root节点是在右子树做完之后才需要回去.
前序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| vector<int> preorderTraversal(TreeNode* root) {
if (root == nullptr)
return {};
vector<int> result;
TreeNode *mostright = nullptr;
while(root != nullptr)
{
if (root->left)
{
mostright = root->left;
while(mostright->right != nullptr && mostright->right != root)
mostright = mostright->right;
if (mostright->right == nullptr)
{
mostright->right = root;
result.emplace_back(root->val);
root = root->left;
}
else
{
mostright->right = nullptr;
root = root->right;
}
}
else
{
result.emplace_back(root->val);
root = root->right;
}
}
return result;
}
|
中序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| vector<int> inorderTraversal(TreeNode* root) {
if (root == nullptr)
return {};
vector<int> result;
TreeNode *mostright = nullptr;
while(root != nullptr)
{
if (root->left)
{
mostright = root->left;
while(mostright->right != nullptr && mostright->right != root)
mostright = mostright->right;
if (mostright->right == nullptr)
{
mostright->right = root;
root = root->left;
}
else
{
result.emplace_back(root->val);
mostright->right = nullptr;
root = root->right;
}
}
else
{
result.emplace_back(root->val);
root = root->right;
}
}
return result;
}
|
后序遍历
后序遍历就是"前序遍历"(中->右->左)的反转.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| vector<int> postorderTraversal(TreeNode* root) {
if (root == nullptr)
return {};
vector<int> result;
TreeNode *mostright = nullptr;
while(root != nullptr)
{
if (root->right)
{
mostright = root->right;
while(mostright->left != nullptr && mostright->left != root)
mostright = mostright->left;
if (mostright->left == nullptr)
{
mostright->left = root;
result.emplace_back(root->val);
root = root->right;
}
else
{
mostright->left = nullptr;
root = root->left;
}
}
else
{
result.emplace_back(root->val);
root = root->left;
}
}
reverse(result.begin(), result.end());
return result;
}
|