堆的结构
同二叉查找树类似, 堆也是一种特殊的二叉树:
- 堆是一颗完全二叉树;
- 堆的孩子结点都小于或者大于父结点;
所以, 堆可以像一颗完全二叉树一样, 很自然地可以使用顺序存储; 区别于二叉查找树, 堆的孩子结点是都小于或者大于父结点.
一般地, 堆划分为小顶堆和大顶堆:
- 父结点小于孩子结点的堆叫做小顶堆;
- 父结点大于孩子结点的堆叫做大顶堆;
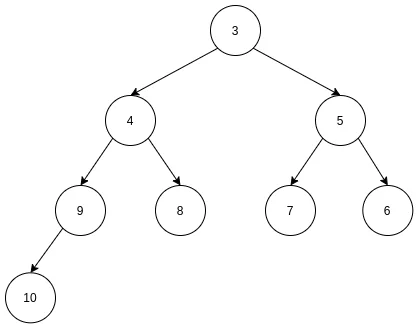
如下是一个小顶堆:
堆-小顶堆
可以化做线形存储:
1
| [3, 4, 5, 9, 8, 7, 6, 10]
|
插入
插入时需要考虑堆的两个条件: 完全二叉树和大小关系.
一种较为简单的插入方式是从下到上插入, 在线形存储中就是在末尾插入:
- 插入到末尾结点;
- 比较与父结点的大小关系;
- 如果不满足大小关系, 则与父结点交换, 回到2, 否则退出;
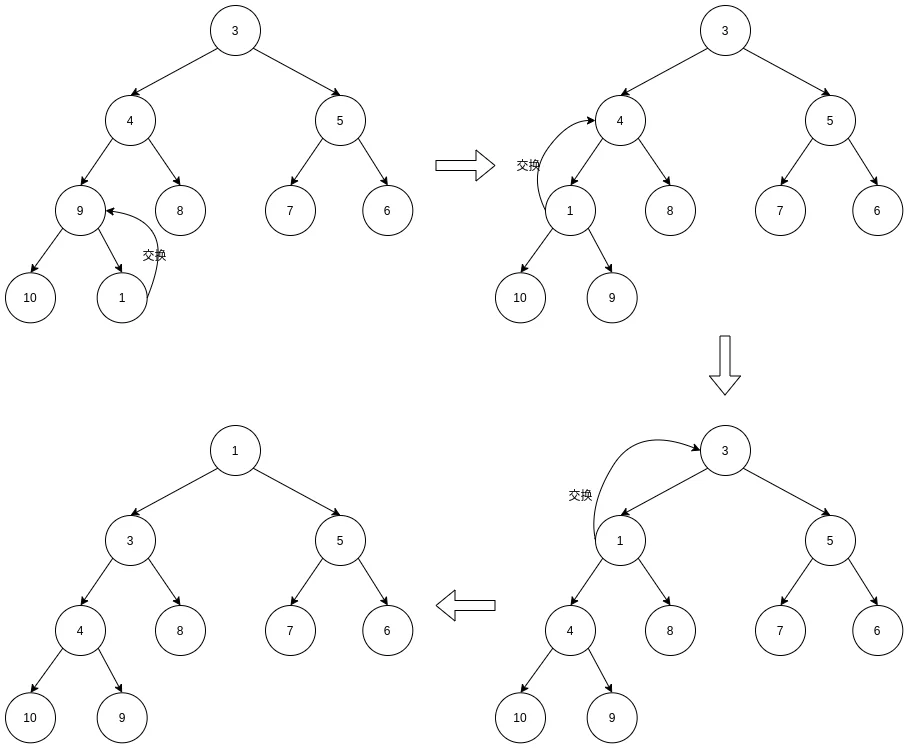
比如对上文的小顶堆插入元素1, 则是如下过程:
堆-插入
对应堆线形存储的插入操作:
待插入元素插入到末尾.
1
2
| // 0 1 2 3 4 5 6 7 8
[ 3, 4, 5, 9, 8, 7, 6, 10, 1]
|
与父结点比较, 父结点index = (8 - 1) / 2 = 3, 不满足大小关系, 交换下标3和8结点.
1
2
| // 0 1 2 3 4 5 6 7 8
[ 3, 4, 5, 1, 8, 7, 6, 10, 9]
|
与父结点比较, 父结点index = (3 - 1) / 2 = 1, 不满足大小关系, 交换下标1和3结点.
1
2
| // 0 1 2 3 4 5 6 7 8
[ 3, 1, 5, 4, 8, 7, 6, 10, 9]
|
与父结点比较, 父结点index = (1 - 1) / 2 = 0, 不满足大小关系, 交换下标0和1结点.
1
2
| // 0 1 2 3 4 5 6 7 8
[ 1, 3, 5, 4, 8, 7, 6, 10, 9]
|
插入结束.
可以知道, 堆的插入操作的复杂度和堆的高度相关, 是$O(logn)$.
删除
堆的删除操作同插入操作类似, 是不断比较和交换的过程.
- 将待删除结点和末尾结点交换;
- 删除末尾结点;
- 比较交换后的结点和孩子结点的关系;
- 如果不满足堆的大小关系, 则与最小/最大的孩子结点交换, 回到3, 否则退出;
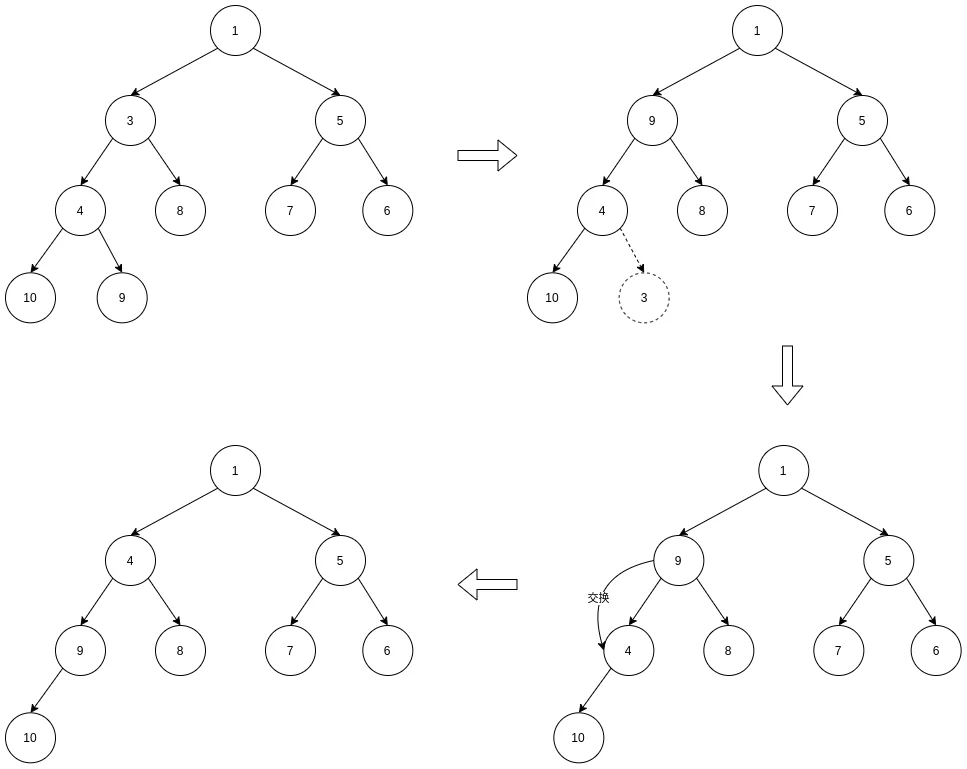
例如删除元素3, 链式结构的删除操作如下:
堆-删除
需要注意的是, 我们需要比较交换后的结点和孩子结点的最小/最大关系, 不需要和父结点比较, 因为和父结点必定是满足大小关系的.
如果是顺序存储:
交换被删除和末尾元素, 交换3和9.
1
2
| // 0 1 2 3 4 5 6 7 8
[ 1, 9, 5, 4, 8, 7, 6, 10, 3]
|
删除末尾元素, 删除3.
1
2
| // 0 1 2 3 4 5 6 7
[ 1, 9, 5, 4, 8, 7, 6, 10]
|
交换后的元素合孩子元素比较, 不满足大小关系, 则和最小的孩子结点交换, 交换9和4.
1
2
| // 0 1 2 3 4 5 6 7
[ 1, 4, 5, 9, 8, 7, 6, 10]
|
C++中的heap
先来看如下一段代码, 使用hp作为待堆化堆数据.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| #include <algorithm>
#include <iostream>
using namespace std;
int main() {
int hp[9] = {1, 3, 4, 5, 6, 7, 8, 9, 10};
using std::begin;
using std::end;
auto php = [&]() {
for_each(begin(hp), end(hp), [](const int &n) { cout << n << " "; });
cout << endl;
};
make_heap(begin(hp), end(hp));
php();
cout << is_heap(begin(hp), end(hp)) << endl;
pop_heap(begin(hp), end(hp));
php();
cout << is_heap(begin(hp), end(hp)) << endl;
hp[8] = 11;
push_heap(begin(hp), end(hp));
php();
cout << is_heap(begin(hp), end(hp)) << endl;
sort_heap(begin(hp), end(hp));
php();
cout << is_heap(begin(hp), end(hp)) << endl;
}
|
输出是
1
2
3
4
5
6
7
8
| 10 9 8 5 6 7 4 3 1
1
9 6 8 5 1 7 4 3 10
0
11 9 8 6 1 7 4 3 5
1
1 3 4 5 6 7 8 9 11
0
|
这里使用了begin和end, 起到迭代器的作用, 可以返回给定容器或者数组的迭代器.
1
2
| using std::begin;
using std::end;
|
begin和end, 是半闭半开的区间, [begin, end). 官网上的图是比较好的解释.
begin和end
make_heap
1
| make_heap(begin(hp), end(hp));
|
将hp指定区间堆化, 如果是begin和end, 则是堆化hp, 默认是大顶堆.
可以接受第三个参数f, 代表堆化规则, 因此可以实现大顶堆/小顶堆, 或者根据指定key堆化.
pop_heap
1
| pop_heap(begin(hp), end(hp));
|
删除堆顶元素, 实际上是将堆顶元素和尾部元素交换, 然后堆化.
需要注意的是, 如上代码pop后, [begin, end)不再满足堆的条件, is_heap返回是false, 但是[begin, end - 1)是一个堆.
push_heap
1
| push_heap(begin(hp), end(hp));
|
push_heap会将末尾堆元素插入堆中, 但是需要保证[begin, end - 1]是一个堆.
sort_heap
1
| sort_heap(begin(hp), end(hp));
|
堆排序, 事件复杂度是稳定的$O(nlogn)$, 相当于:
1
| pop_heap(begin(hp), end(hp) - i);
|
is_heap
1
| is_heap(begin(hp), end(hp));
|
判断[begin, end)是否满足堆条件.
