数据结构与算法之图

2021-03-09 约 2355 字预计阅读 5 分钟

什么是图

在前面的文章中, 我们了解了树的概念, 重点是二叉树, 图在拓扑结构上和树有点类似, 但是图不是树.

直观地, 先来看一个图的拓扑结构:

https://bu.dusays.com/2022/06/26/62b87f3a92fc5.png — 无向图

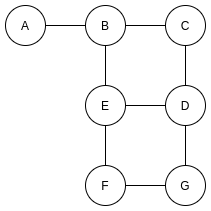
上述展示的是无向图, 无向图就是没有方向的图, 只要两个结点之间是联通的, 就可以从一个结点到另外一个结点.

我们可以将其理解为简化后的地图, A-G代表的是地点.

一般地, 对图我们有以下的一般性概念:

图的结点叫做顶点;
顶点(结点)之间的连接叫做边;
一个顶点(结点)有多少条边叫做这个顶点(结点)的度;

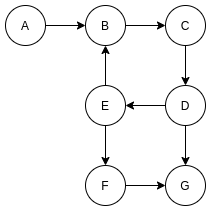
对应的, 还有有向图, 有向图就是有方向的图, 链接的两个顶点的边有方向, 可以从一个顶点到另外一个顶点, 如果两个顶点互通, 则至少要有两条不同方向的边.

有向图类似于行车单向道.

https://bu.dusays.com/2022/06/26/62b87f3cdfbd9.png — 有向图

有向图的边可能从一个顶点指出, 也可能指向一个顶点, 我们把从顶点指出的边的数量叫做这个顶点的出度, 指向一个顶点的边的数量叫做这个顶点的入度.

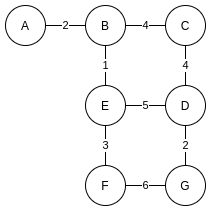
类比于地图, 两顶点之间的边不仅可以表示联通关系, 还可以表示距离, 给每条边带上一个"距离"参数(权重), 这样的图叫做带权图:

https://bu.dusays.com/2022/06/26/62b87f3f0b784.png — 带权图

图的类比对象

用图这种数据结构可以表示日常生活中的一些常用对象, 这里举一些例子:

地图可以用图表示, 顶点就是地点, 边就是两个地点之间的路径, 边带上权重就可以表示距离;
好友关系也可以用图表示, 顶点就是每个个体, 边表示这两个个体之间是否有联系, 边带上权重可以表示好感度;
编译器也用到了图, C/C++编译时的头文件include就可以用图的顶点表示, 有向边可以表示依赖关系;

邻接表存储法

图如何存储?

很直观的时类似树一样的存储方法, 用链表表示图的拓扑结构. 但是这种方法的问题在于不知道图的每个顶点会有多少条边, 所以不太好定义结构体.

邻接表存储法也是使用链表存储的方法, 它把每个顶点表示为链表的头, 后继结点则是与顶点连接的其他顶点, 如下图表示无向图的邻接表存储法:

https://bu.dusays.com/2022/06/26/62b87f42a914f.png — 邻接表存储法

1
2
3
4
5
template <typename T>
struct Graph{
    T val;
    vector<Graph<T>*> link;
};

以上, val表示顶点的值, link中则是存与这个顶点联通的其他顶点.

这里的link看起来是顺序存储, 如果查找与顶点连接的某个其他顶点时, 时间复杂度时$O(n)$, 我们可以使用查找二叉树或者红黑树等结构来替代顺序结构, 提高查找效率, 具体使用的数据结构还需根据具体场景分析.

广度优先搜索(BFS)

图的搜索/遍历和树类似, 需要注意的就是图可以有回环, 不要陷入死循环即可.

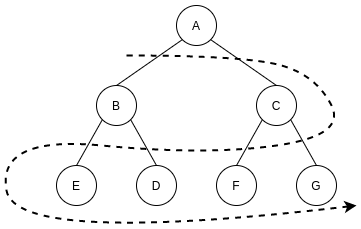
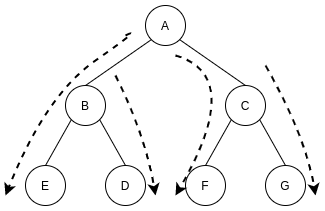
广度优先搜索是先访问起始结点的所有子结点, 再访问子结点的所有子结点, 从树的结构来看, 是一层一层的访问.

下面我们用树的结构来展示一下BFS是怎么搜索的:

https://bu.dusays.com/2022/06/26/62b87f45816f3.png — BFS

先定义图的结构:

1
2
3
4
5
6
7
8
template <typename T>
struct Graph{
    T val;
    vector<Graph<T>*> link;

    Graph(const T& v) : val(v) {}
};
using Map = Graph<char>;

我们的主函数, 使用上文中的无向图:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
int main()
{
    vector<vector<char>> link_map{
        {'A', 'B'},
        {'B', 'A', 'C', 'E'},
        {'C', 'B', 'D'},
        {'D', 'C', 'E', 'G'},
        {'E', 'B', 'D', 'F'},
        {'F', 'E', 'G'},
        {'G', 'D', 'F'},
    };

    auto graph = initGraph(link_map);

    return 1;
}

link_map的条元素的第一个元素代表顶点, 之后的元素则代表与该顶点连接的其他顶点;

编写一个图打印函数, 用来输出使用邻接表存储法的图:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
void printGraph(const vector<Map> &graph)
{
    using std::begin;
    using std::end;
    for_each(begin(graph), end(graph), [](auto& g){
        cout << g.val << "(" << &g << ")";
        auto &link = g.link;
        for_each(begin(link), end(link), [](auto& l){
            cout << "->" << l->val << "(" << l << ")";
        });
        cout << endl;
    });
}

将图的初始化数据转化为邻接表存储:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
vector<Map> initGraph(const vector<vector<char>> &link_map)
{
    using std::next;
    using std::begin;
    using std::end;

    vector<Map> graph;
    unordered_map<char, int> map_map;
    int pos = 0;
    for (auto &link : link_map)
    {
        const char& c = link[0];
        Map g(c);
        graph.emplace_back(g);
        map_map.emplace(c, pos++);
    }

    auto g = begin(graph);
    for (auto &link : link_map)
    {
        for_each(next(begin(link)), end(link), [&](auto& c){
            pos = map_map[c];
            auto pg = &graph[pos];
            g->link.emplace_back(pg);
        });
        g = next(g);
    }

    printGraph(graph);

    return graph;
}

初始化graph后, 我们得到输出:

1
2
3
4
5
6
7
A(0x11852a0)->B(0x11852c0)
B(0x11852c0)->A(0x11852a0)->C(0x11852e0)->E(0x1185320)
C(0x11852e0)->B(0x11852c0)->D(0x1185300)
D(0x1185300)->C(0x11852e0)->E(0x1185320)->G(0x1185360)
E(0x1185320)->B(0x11852c0)->D(0x1185300)->F(0x1185340)
F(0x1185340)->E(0x1185320)->G(0x1185360)
G(0x1185360)->D(0x1185300)->F(0x1185340)

针对广度优先搜索算法, 我们使用open-close表实现.

open表中存储接下来需要访问的结点, 一般可以用双端队列;
close表中存储已经访问过的结点, 一般可以用任意容器;

接下来确定对每个结点的操作:

判断结点是否已经被访问过(是否在close表中):

1
2
3
4
5
6
7
8
using std::begin;
using std::end;
auto isInClose = [&vclose](auto& node){
    auto node_pos = find_if(begin(vclose), end(vclose), [&](auto& cnode){
        return cnode == node;
    });
    return node_pos != end(vclose);
};

将接下来需要访问的结点放到open表:

1
2
3
auto openPush = [&vopen](auto& node){
    vopen.emplace_back(node);
};

从open表中取出结点, 并访问:

1
2
3
4
5
auto openGet = [&vopen](){
    auto node = vopen.front();
    vopen.pop_front();
    return node;
};

这里要注意open表的操作, push的时候是将结点push到末尾, 取元素时则是从头开始取.

对结点处理, 简单起见, 这里使用cout

1
2
3
auto processNode = [](auto& node){
    cout << node->val << " ";
};

有了上述基本操作, 广度优先遍历实现如下:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
void algoBFS(vector<Map>& graph)
{
    deque<Map*> vopen;
    vector<Map*> vclose;

    auto isInClose = [&vclose](auto& node){
        auto node_pos = find_if(begin(vclose), end(vclose), [&](auto& cnode){
            return cnode == node;
        });
        return node_pos != end(vclose);
    };

    auto openPush = [&vopen](auto& node){
        vopen.emplace_back(node);
    };

    auto openGet = [&vopen](){
        auto node = vopen.front();
        vopen.pop_front();
        return node;
    };

    auto processNode = [](auto& node){
        cout << node->val << " ";
    };

    auto node = &graph[0];
    openPush(node);
    do{
        node = openGet();
        if(!isInClose(node))
        {
            processNode(node);
            vclose.emplace_back(node);
            for(auto& l : node->link)
            {
                if (!isInClose(l))
                {
                    openPush(l);
                }
            }
        }
    }while(!vopen.empty());
}

输出得到:

1
A B C E D F G

深度优先搜索(DFS)

深度优先搜索从树的结构来看就是从根结点一直访问到叶子结点.

下面我们用树的结构来展示一下DFS是怎么搜索的:

https://bu.dusays.com/2022/06/26/62b87f48456a7.png — DFS

深度优先搜索的逻辑和广度优先搜索基本一样, 区别在于从open表中取值的方式不同.

在广度优先搜索中, 我们将待访问结点push到open表的末尾, 再从open表的表头拿下一个访问的结点, 这样的结果就是先访问了结点的所有子结点, 再访问子结点的所有子结点.

深度优先搜索是将待访问结点push到open表的末尾, 再从open表的末尾拿下一个访问的结点, 这样相当于是从一个几点一直追溯子结点, 直到末尾, 如此往复.

以下是深度优先搜索中的openGet操作:

1
2
3
4
5
auto openGet = [&vopen](){
    auto node = vopen.back();
    vopen.pop_back();
    return node;
};

完整实现如下:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
void algoDFS(vector<Map>& graph)
{
    deque<Map*> vopen;
    vector<Map*> vclose;

    using std::begin;
    using std::end;
    auto isInClose = [&vclose](auto& node){
        auto node_pos = find_if(begin(vclose), end(vclose), [&](auto& cnode){
            return cnode == node;
        });
        return node_pos != end(vclose);
    };

    auto openPush = [&vopen](auto& node){
        vopen.emplace_back(node);
    };

    auto openGet = [&vopen](){
        auto node = vopen.back();
        vopen.pop_back();
        return node;
    };

    auto processNode = [](auto& node){
        cout << node->val << " ";
    };

    auto node = &graph[0];
    openPush(node);
    do{
        node = openGet();
        if(!isInClose(node))
        {
            processNode(node);
            vclose.emplace_back(node);
            for(auto& l : node->link)
            {
                if (!isInClose(l))
                {
                    openPush(l);
                }
            }
        }
    }while(!vopen.empty());
}

输出得到:

1
A B E F G D C