数据结构与算法之跳表

一维链表

链表不需要一块很大的连续的存储空间是其优点, 但是对一串有序序列, 使用一维链表查询的时间复杂度是$O(n)$, 能否如查找二叉树之类, 将其查找时间复杂度降为$O(logn)$呢?

一种常用的方法是升维. 升维也是一种空间换时间的思考方式, 会提高数据结构的空间复杂度, 但是可以降低一些操作的时间复杂度.

跳表

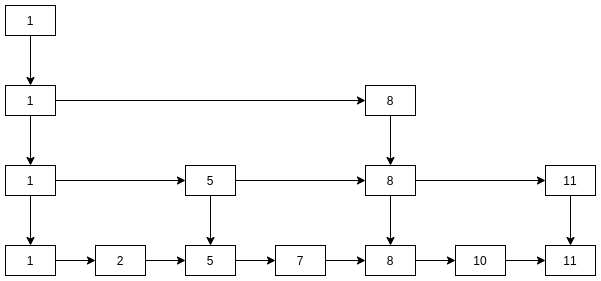
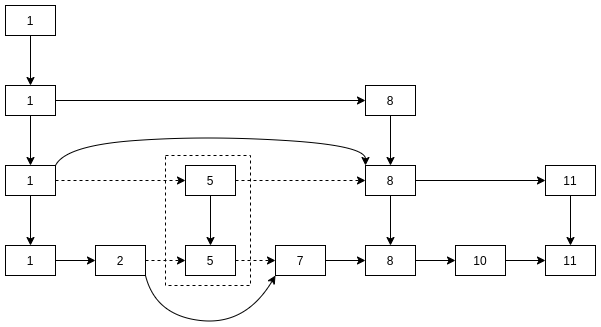
跳表的一般结构, 将一维链表升维成二维:

跳表类似于图书馆的图书管理结构. 一般地, 图书馆存放图书有以下约定:

1. 每本图书有其对应的唯一ID(key);
2. 每本图书的ID可以比较大小关系;
3. 图书是按照ID顺序存放的;
4. 每一段ID的图书会放到同一个书架;
5. 每个书架标识了存放图书的ID范围;

我们人工找书的操作是:

1. 确定需要查找的图书的ID;
2. 将图书ID与每个房间的最大最小ID比较, 如果在范围内则进入房间查找, 否则继续遍历下一个房间;
3. 进入房间后, 将图书ID与每个书架的最大最小ID比较, 如果在范围内则进入书架查找, 否则继续遍历下一个书架;
4. 走到对应书架, 按照顺序遍历书架上的每本书的ID, 如果与待查ID匹配则找到, 否则, 继续查找下一本书, 如果该书架所有书遍历完没找到, 则不存在;

放在跳表中, 这个数据结构是这样的:

1. 每本书: 这里存储了每本书的ID(Key), 和书的内容;

   

2. 每个书架: 这里只存储书ID范围, 可以不包括书的内容;

   

3. 每个房间: 这里只存储书ID范围, 可以不包括书的内容;

   

4. 每栋楼: 这里只存储书ID范围, 可以不包括书的内容;

   

查找

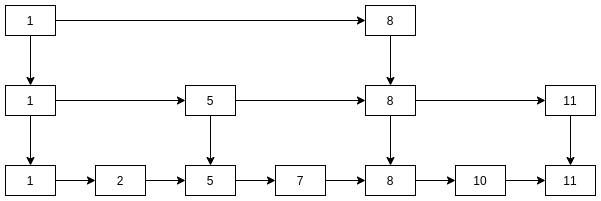
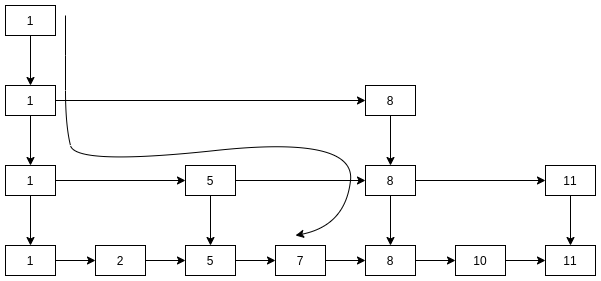
比如, 按照上文的数据, 查找元素7的流程是:

1. 7与1判断, 7比1大, 且第四层1没有后继, 转第三层;
2. 7与8比较, 比8小, 且8的前驱是1, 转第二层;
3. 7与5比较, 7比5大, 且5的后继是8, 转第一层;
4. 7与7比较, 匹配, 退出.

在这里我们规定, 跳表的层级结构是从下往上的, 即每本书是第一层, 每栋楼是最高层.

按照这种结构(跳表), 对$N$个有序数据, 我们可以将连续$S$个数据划分为一组, 又将$S$个组划分为一个大组, 以此类推.

可以知道, 这种"组"的层数和每个组的成员数目有关, 为$log_S N$.

每次查找操作的时间复杂度是$O(S)$.

所以, 跳表的查找时间复杂度是$O(Slog_SN)$, $S$一般是常数, 即查找时间复杂度是$O(logn)$.

跳表需要用到额外的索引, 如果取$S = 2$, 可以知道额外的索引空间是 $\lim\limits_{N\rightarrow\infty}\sum_1 ^N \frac{N}{2^i} = N$, 如果$S$越大, 则需要越少的额外空间, 所以跳表的空间复杂度是$O(n)$.

插入

按照查找操作找到待插入数据的位置, 之后插入即可. 但是这样可能带来退化的问题, 如果大量数据插入, 而我们没有更新索引, 则会导致跳表退化成链表(时间复杂度接近链表).

为了解决插入导致的退化问题, 我们需要在插入的时候, 动态更新索引, 比较常规的规则是:

根据某种条件, 确定待插入的结点是否要构建索引.

比如按照随机数规则, 如果rand(1, 10) <= 1, 则对当前插入元素建立索引, 从多少层元素开始建立索引呢? 也可以根据随机数来确定, 从第k = rand(2, log(N))层开始建立索引.

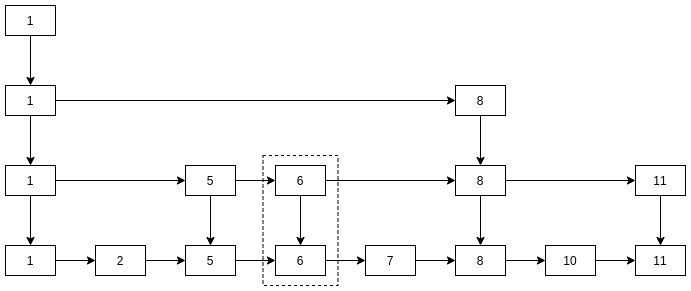
以下, 插入元素6, 从第二层开始建立索引.

当然, 我们也可以按照其他规则建立索引, 根据数据与项目的规则, 比如:

1. 根据数据奇偶性;
2. 根据某哈希函数(奇偶性判断也可以理解为哈希);
3. 根据已插入结点的数目;

删除

和链表操作一样, 直接删除元素即可, 但是需要注意, 如果有上级索引, 则也要删除上级索引.

同样, 如果过多删除索引结点, 也可能引起跳表的退化. 类比于动态更新索引的操作, 删除操作时也可以制定一些规则来动态更新索引, 比如:

1. 如果删除结点是索引结点且前驱/后继结点存在, 则可以对前驱/后继结点建立索引, 索引深度和被删除结点一致;
2. 同1, 但是加入随机数判断是否对前驱/后继结点建立索引;
3. 同1, 但是加入随机数计算前驱/后继结点建立索引的深度;