先约定两个概念, 主串和模式串.
比如在S字符串中查找s字符串, 则S是主串, s是模式串.
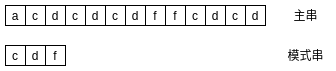
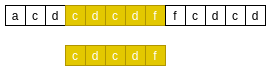
如下, 在主串中搜索"cdf"模式串:
主串和模式串
BF
暴力匹配是很朴素的字符串匹配算法, 将主串中的字符与模式串的字符一个一个匹配, 如果遇到不匹配的字符对则主串向后滑动一个字符, 从头开始匹配:
暴力匹配
代码实现如下, strStr的作用是从haystack字符串中找到needle字符串首次出现的位置, 如果没有找到则返回-1. (LC.28)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| int strStr(string haystack, string needle)
{
if (needle.empty())
return 0;
int sh = haystack.size();
int sn = needle.size();
if (sh < sn)
return -1;
for (int i = 0; i <= (sh - sn); i++)
{
int j = 0;
for (; j < sn; j++)
{
if (haystack[i + j] != needle[j])
{
break;
}
}
if (j >= sn)
{
return i;
}
}
return -1;
}
|
记主串长度为m, 模式串长度为n, 可以得到暴力匹配的时间复杂度是$O(mn)$, 空间复杂度是$O(1)$;
BM
暴力匹配没有用到主串的一些先验信息. 假设模式串首字符是’a’, 我们可以记住主串中’a’出现的位置, 然后用主串中’a’出现的位置与模式串匹配, 这样可以减少一些比较次数. (实际上最差时间复杂度也没有提高.)
接下来的BM就用到了主串和模式串中的一些先验信息, 提高空间复杂度, 但是降低了时间复杂度, 不同于暴力匹配, BM算法是从右向左遍历. 为什么需要从右向左遍历呢? 先来看看BM算法的两条规则.
坏字符原则
对模式串, 从右向左匹配, 如果是错误匹配, 则记主串的字符a, 在模式串中从右向左查找下一个与主串字符a匹配的字符, 再将模式串移动到这个位置. 如果没有找到, 则将整个模式串移动到这个字符后面.
如下:
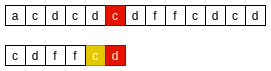
- 从右向左, 主串’d’与模式串’f’不匹配, 则在模式串中从右向左找到下一个与主串’d’匹配的字符;
- 将模式串的下一个与主串’d’匹配的字符对齐;
BM-坏字符原则一
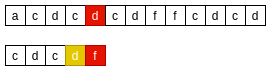
- 从右向左, 主串’c’与模式串’f’不匹配, 则在模式串中从右向左找到下一个与主串’c’匹配的字符;
- 将模式串的下一个与主串’c’匹配的字符对齐;
BM-坏字符原则二
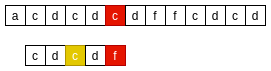
- 模式串匹配成功.
BM-坏字符原则三
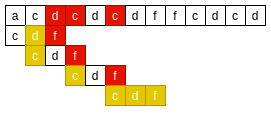
对BF中匹配的例子来说, 使用BM的坏字符原则, 可以减少匹配次数:
- 从右向左, 主串’d’与模式串’f’不匹配, 则在模式串中从右向左找到下一个与主串’d’匹配的字符;
- 将模式串的下一个与主串’d’匹配的字符对齐;
- 从右向左, 主串’c’与模式串’f’不匹配, 则在模式串中从右向左找到下一个与主串’c’匹配的字符;
- 将模式串的下一个与主串’c’匹配的字符对齐;
- 从右向左, 主串’c’与模式串’f’不匹配, 则在模式串中从右向左找到下一个与主串’c’匹配的字符;
- 将模式串的下一个与主串’c’匹配的字符对齐;
- 模式串匹配成功.
BM与BF比较
再看一个特殊的例子:
首先, 按照坏字符原则, 从右向左, 主串’d’与模式串’c’不匹配, 则在模式串中从右向左找到下一个与主串’d’匹配的字符, 没有找到则将模式串移动到主串’d’后面:BM-坏字符原则三接下来主串’c’与模式串’c’匹配, 但是主串’d’与模式串’f’不匹配, 且在子串中找不到下一个’d’, 这时候我们依然可以按照坏字符原则移动模式串, 但是主串’c’与模式串’c’匹配这条信息却没有用上.
有没有办法用上已经匹配的子串信息呢? 这就是BM算法的好前缀原则.
好前缀原则
先看一个例子, 匹配以下字符串:BM-好前缀原则一首先我们可以按照坏后缀原则匹配, 移动模式串后, 发现已经有一段子串是匹配好的, 这时候可以触发好前缀原则.
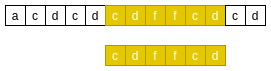
如下, 模式串的"cd"和主串的"cd"匹配, 但是主串’d’与模式串’f’不匹配, 这时候在模式串中从右向左查找下一个"cd"子串, 如果查找到, 则将模式串的下一个"cd"子串与主串"cd"子串对齐.BM-好前缀原则二
现在匹配成功了.BM-好前缀原则三
如果模式串中没有查找到下一个与"cd"匹配的子串呢? 这时候需要分两种情况考虑:
- 模式串头有子串的子串, 则将模式串头子串的最大子串与主串的子串对齐;
- 模式串头没有子串的子串, 则将模式串移动到主串的子串的后面.
如下例子:
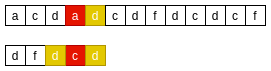
主串’d’与模式串’d’匹配, 主串’a’与模式串’c’不匹配, 则在模式串中查找下一个与"d"匹配的子串, 并与主串对齐:BM-好前缀原则四
主串’dcd’与模式串’dcd’匹配, 主串’a’与模式串’f’不匹配, 模式串中没有查找到下一个与"dcd"匹配的子串, 但是模式串头的"d"是子串"dcd"的子串, 所以将"d"对齐:BM-好前缀原则五
问题: 为什么与末尾的"d"对齐而不是与第一个"d"对齐呢?
如果与第一个"d"对齐, 模式串中势必没有第二个"dcd"子串, 所以一定是不匹配的, 直接与末尾"d"对齐就可以了.
对BM两条原则的思考
对坏字符或者好前缀原则, 从右往左匹配可以让我们移动最少的距离, 防止错过一些匹配.
如果坏字符所在子串可能和模式串匹配, 则模式串中一定有一个和坏字符匹配的字符. 所以坏字符原则只是尝试以下这种可能.
同问题二, 如果好前缀是可能的匹配, 则模式串中一定有另一个匹配的后缀或者后缀子串.
按照问题一的解释, 则两个原则都是在保证有一定匹配串的情况下, 移动尽量小的距离, 单独使用某一种原则再加上一些边界处理条件也可能完成匹配过程, 为了算法加速, 则可以使用坏字符和好前缀中移动距离最长的结果.
如果遇到坏字符, 并且找到了与坏字符匹配的其他字符的情况下, 是可以正常使用坏字符原则的. 如果没有找到呢? 不管有没有好前缀, 将模式串移动到坏字符后面重新尝试匹配就可以了.
同坏字符原则, 如果有匹配则正常匹配, 如果没有匹配则将匹配串移动到好后缀后面即可.
BM代码实现
坏字符的代码实现
坏字符原则的朴素实现比较简单, 每次遇到坏字符, 对模式串从右向左找到下一个与坏字符匹配的字符即可. 但是这样的操作效率十分低下. 因为是在模式串中查找一个字符, 我们可以考虑用一个map记录字符在模式串中最后的位置:
1
2
3
4
5
6
7
8
9
| void badChar(unordered_map<char, int> &badmps, const string &pstr)
{
int size = pstr.size();
for (int i = 0; i < size; i++)
{
//badmps代表的是模式串的字符的最右位置
badmps[pstr[i]] = i;
}
}
|
再提供一个函数计算移动距离:
1
2
3
4
5
6
7
| int badMove(unordered_map<char, int> &badmps, const char &badc, const int &pos)
{
//尽管可能是负数, 但是我们并不是很当心
//1. 负数可以用右移一位代替
//2. 增加复杂度, 不匹配模式串最右匹配, 而是匹配模式串以坏字符为界的右子串的最右匹配
return badmps.find(badc) != badmps.end() ? pos - badmps[badc] : -1;
}
|
好前缀的代码实现
好前缀原则我们需要实现两个地方:
- 最右的与好前缀完全匹配的子串;
- 如果没有完全匹配的子串, 则找到头部的部分匹配的子串.
参考一般解法, 可以实现如下的代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| void goodMatch(vector<int> &sufix, vector<bool> &prefix, const string &pstr)
{
int size = pstr.size();
sufix.reserve(size);
prefix.reserve(size);
for (int i = 0; i < size; ++i)
{
//sufix[i]表示长度为i的子串的位置, 需要注意, 长度为i的子串是唯一的.
//-1则时不存在这个子串
sufix[i] = -1;
//prefix[i]表示这个子串是不是在头部
prefix[i] = false;
}
int pstr_max_index = size - 1;
//不需要遍历整个模式串, 因为长度满的时候, 必定没有其他子串
for (int i = 0; i < pstr_max_index; i++)
{
//是遍历的初始位置, 从右向左
int j = i;
//k用来记录子串的长度
int k = 0;
//这样我们拿到的sufix总是最右的
while ((j >= 0) && (pstr[j] == pstr[pstr_max_index - k]))
{
sufix[++k] = j--;
}
if (j < 0)
{
prefix[k] = true;
}
}
}
|
为什么这么做?
因为待匹配的子串是已知的, 就是模式串的子串, 所以在预处理的时候获得这些一直子串的位置就可以在处理的时候减少一些计算, 降低时间复杂度.
做完预处理之后, 还需要一个函数计算偏移量:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| int goodMove(const vector<int> &sufix, const vector<bool> &prefix, const int &mlen, const int &pos)
{
if (mlen < 1)
return -1;
int move_len = 0;
int size = sufix.size();
move_len = sufix[mlen];
if (move_len < 0)
{
for (int i = mlen - 1; i > 0; i--)
{
if (prefix[i] == true)
{
move_len = sufix[i];
break;
}
}
}
return pos - move_len;
}
|
BM完整代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| int strStr(string haystack, string needle)
{
//边界条件比较少, 先处理一下
if (needle.empty())
return 0;
int sh = haystack.size();
int sn = needle.size();
if (sh < sn)
return -1;
//预处理
unordered_map<char, int> badmps;
badChar(badmps, needle);
vector<int> sufix;
vector<bool> prefix;
goodMatch(sufix, prefix, needle);
int i = 0;
while (i <= (sh - sn))
{
int j = sn - 1;
int mlen = 0;
char bad_char = 0;
while (j >= 0)
{
if (haystack[i + j] != needle[j])
{
bad_char = haystack[i + j];
break;
}
mlen++;
j--;
}
if (mlen >= sn)
{
return i;
}
//拿到不匹配字符的位置
int pos = sn - mlen - 1;
int bad_step = badMove(badmps, bad_char, pos);
int good_step = goodMove(sufix, prefix, mlen, pos);
int step = max(bad_step, good_step);
if (step < 0) step = sn;
i += (step > 0 ? step : 1);
}
return -1;
}
|
