Bing's Blog
归档
标签 分类
友链
更多
工具 关于 建站 RSS
Bing's Blog

《UCB CS61a SICP Python 中文》一周目笔记(一)

   约 3246 字   预计阅读 7 分钟 

UCB SICP译文, 看这里.

令我印象深刻的是MIT SICP第一章中的例子题1.5:应用序和正则序.

使用函数构建抽象

第一大章初会觉得很简单, 但是仔细看还是可以看到很多忽略的知识点, 比如我印象最深的, 对调用栈的解释, 这里用的名词是环境(应该是一个意思).

中缀记号和函数

一个很容易观察到, 但是容易被忽略的问题:

1
2
3
4

>>> 2 + 3
5
>>> add(2, 3)
5

在简短的表达式中, 2 + 3是很容易被使用的. 但是2 + 3和add(2, 3)的区别我却没有花心思去考虑过:

  1. 2 + 3仅适合两个元素;

  2. add可以适应任意多个元素;

当然, 并不是说都需要将中缀记号替换为函数, 这本来就是不合理的. 比如说:

对于简单的算术运算, Python 在惯例上倾向于运算符而不是调用表达式.

这里仅仅是让你注意到这一点. 在后面章节中会提到add函数的其他优点.

全局环境和局部环境

  1. 实参是怎么传入到形参的?

  2. 形参为什么可以重名?

全局环境(帧)

内建函数/用户定义的全局变量/用户定义的全局函数等等, 会作为全局环境的组成部分.

https://wizardforcel.gitbooks.io/sicp-py/content/img/global_frame_assignment.png

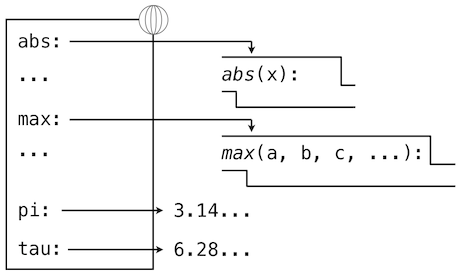
如上图, 表示一个全局环境, 其中pi/tau等变量是通过导入和赋值加入到全局环境中的.

赋值和导入语句会向当前环境的第一个帧添加条目

根据上面这个原理, 当前环境是全局环境, 所以导入和赋值引入的变量等名字将会导入到当前环境中, 也就是全局环境.

局部环境(帧)

比如这样一个函数:

1
2

>>> def square(x):
        return mul(x, x)

将会有自己的局部环境, square的环境和全局环境是不一样的, 但是全局环境可以指向这个局部环境.

比如下图, 虽然都有一个叫做x的东西, 但是他们在不同的局部环境, 所以不会互相干扰.

https://wizardforcel.gitbooks.io/sicp-py/content/img/global_frame_def.png

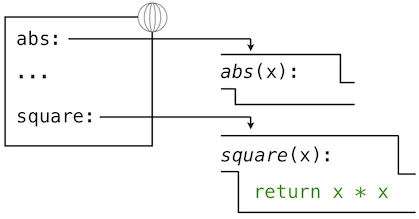
那么, 上述square函数的局部环境如何?

https://wizardforcel.gitbooks.io/sicp-py/content/img/evaluate_square.png

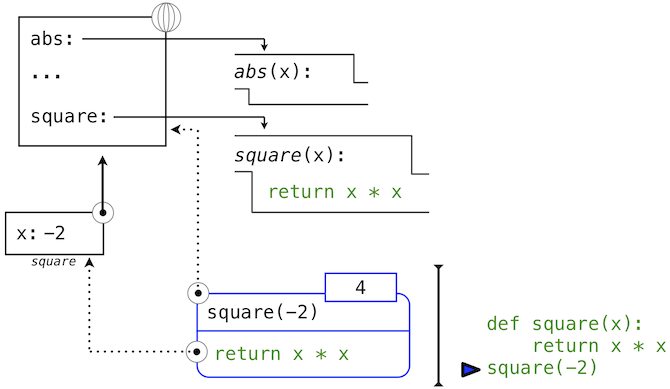
上述调用过程总结如下:

  1. 在全局环境中计算表达式-2的结果;
  2. 在全局环境中搜索square;
  3. 切换到square局部环境, 发现x, 将-2绑定到x;
  4. 在当前环境(square局部环境)计算x*x;
  5. 退出到全局环境, square计算结果输出到全局环境.

小结

关于环境, 看做是一个映射表, 全局环境或这局部环境都是key(名字), value(真正的内容)会指向其他地方, 在同一个环境中, 只需要关系key不一样就可以了, 不关心value是不是一样.

  • 问题1: 实参是怎么传入到形参的?

实参在函数的局部环境中被绑定到形参上.

  • 问题2: 形参为什么可以重名?

因为采用了局部环境, 在不同的环境中, 相同的名字不影响.

函数抽象

  1. 函数抽象举例.
  2. 为什么要做函数抽象?

黑盒

以下例子令我有种醍醐灌顶的感觉:

1
2
3
4

def square(x):
        return mul(x, x)
def square(x):
        return mul(x, x-1) + x

函数返回的结果一样, 但是里面实现不一样. 这就是黑盒. 实际上, 我认为我们确实应该把函数当做黑盒. 但是实现起来并没有那么容器.

举例C++的STL, 每个容器的实现都当做黑盒, 所以如果某某能知道各种STL函数, 但是不理解里面的实现, 也没什么了不起的啦. 黑盒确实没必要过分探究.

再说STL, 实际上我们也不是完全不需要关系黑盒内部. 比如vector/list等, 在某些需求下, 可以认为是对等关系的, 但是我们用户却需要考虑到这些容器的内部实现, 以做出更佳的选择, 比如遇到多线程问题时, vector可能需要被慎重考虑了. 所以STL在使用上, 也不是那么的"无脑".

这里给我的提示就是:

用户不应该需要知道如何实现来调用.

这句话是值得思考的, 我的理解是:

  1. 用户不需要知道内部实现(通俗的理解);
  2. 用户不会惊讶于函数的返回(黑盒函数的返回值是正常的可以理解的, 而不会放回一些意外的东西);
  3. 用户不会惊讶于函数的输入(类似2, 函数的输入是合乎常理的, 不会有意外的输入, 下面我会举一个真实的例子).
一个反例

某同事期望定制一个基类, 并且他将类定义为了模板类. 他的问题是, 模板并不能代表这个类的意义, 仅是为了其中某些成员函数而引入了模板.

将STL作为对比, 使用vector等容器的时候, 传入int等模板是有意义的, 它告诉你这是一个int容器. 或者放开想象, 可以直接将vector看成某种特殊的int, 因为这时候的vector<int>我们就是在当做一个int在做.

但是他的做法, 使用模板类, 但是模板类的模板只是指代类中某些个函数的输入类型, 和这个类完全没关系.

比如说:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

template <typename T>
class A{
public:
	//...
	T get(){ //... }
	void set(const T& t) { //... }

private:
	_container<T> m_data;
}

以上, 我认为是一个好的定义, 模板T代表这个类的类型, 用户操作这个类的时候, 就像在操作T一样, 因为get的返回和set的输入都是T, 并且其中主要参与作用的数据也是T(m_data, 当然底层数据是用户无需关心的.)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

template <typename T>
class A{
public:
	//...
	int get(){ //... }
	void set(const T& t) { //... }

private:
	_container<int> m_data;
}

以上, 引入了模板T, 但是这个的表现并不像T, 因为get的返回和T无关, set的输入虽然是T, 但是和这个类无关, 因为这个类的主要数据m_data的类型是int. 这就是不好的做法, 为了用模板而用模板. 这就不是一个黑盒!

什么应该抽象为函数

这个应该好好想想. 我以及我周围很多人都做不好. 要不是抽象的部分太大, 要不是抽象的部分太特殊以至于只有写的人自己用了.

这个例子我认为挺好的:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

>>> def pressure(v, t, n):
        """Compute the pressure in pascals of an ideal gas.

        Applies the ideal gas law: http://en.wikipedia.org/wiki/Ideal_gas_law

        v -- volume of gas, in cubic meters
        t -- absolute temperature in degrees kelvin
        n -- particles of gas
        """
        k = 1.38e-23  # Boltzmann's constant
        return n * k * t / v

可以看出来, 这里是某个公式. 如果直接把公式写出来, 外行人非常容易疑惑, 但是抽象为函数, 则容易理解多了. 这也是一个黑盒.

另外不仅仅是抽象为函数, 也可以是一个变量:

1

pressure = #...

变量做法我在一些判断式中经常用. 比如:

1
2
3

if( exp1 && exp2 && exp3 ){
    // ...
}

这里的exp*应该抽象出来, 指代每一个exp的具体含义, 比如:

1
2
3
4
5
6

is_range_ok = //...
is_size_ok = //...
is_empty = //...
if (!is_empty && is_range_ok && is_size_ok) {
	// ...
}

这时候会容易理解多了.

其实还没有解答我的问题, 可能这是一个经验性的问题吧~ 以上例子仅做参考, 不同的人可能有不同的想法.

小结

  1. 怎么写黑盒? 就是让黑盒的行为不超出用户的意外, 输入输出看起来都很自然.
  2. 函数抽象也应该像黑盒一样, 不仅仅是将一段重复使用的代码写成函数就好了.

高阶函数

  1. 高阶函数概念.
  2. 高阶函数举例.

第一小节我们提到了add函数, 实际上add是一个很宽泛的行为. 我们可以直接add, 也可以是绝对值add, 平方值add等等. 这里就涉及到了高阶函数.

推荐阅读MIT的SICP(我还没看完…), 在LISP里面使用高阶函数看起来太自然了, 在Python中多多少少有点别扭…

我们需要思考的问题是:

为什么要使用高阶函数? 什么时候应该用高阶函数?

参数是函数

摘抄原文的三个求和的例子:

1
2
3
4
5
6
7

>>> def sum_naturals(n):
        total, k = 0, 1
        while k <= n:
            total, k = total + k, k + 1
        return total
>>> sum_naturals(100)
5050

1
2
3
4
5
6
7

>>> def sum_cubes(n):
        total, k = 0, 1
        while k <= n:
            total, k = total + pow(k, 3), k + 1
        return total
>>> sum_cubes(100)
25502500

1
2
3
4
5
6
7

>>> def pi_sum(n):
        total, k = 0, 1
        while k <= n:
            total, k = total + 8 / (k * (k + 2)), k + 4
        return total
>>> pi_sum(100)
3.121594652591009

以上三个函数实现了不同的功能, 但是仔细观察可以发现, 函数的抽象功能是一样的. 总结就是:

1
2
3
4
5

def <name>(n):
    total, k = 0, 1
    while k <= n:
        total, k = total + <term>(k), <next>(k)
    return total

不同的仅仅是term和next, 一个用于计算部分结果, 一个用于返回下一个值.

最外层函数也是有意义的, 它的作用是计算 $$ s(N) = \sum_{i=1, k=f(i)}^{N}{g(k)} $$ 所以, 这三个例子相当于是三个函数的组合, 最外层的$s$, 以及内层的$f$和$g$.

返回是函数

例子:

1
2
3
4
5
6
7

>>> def compose1(f, g):
        def h(x):
            return f(g(x))
        return h
>>> add_one_and_square = compose1(square, successor)
>>> add_one_and_square(12)
169

读懂例子并不难, 但是要好好理解. 那上三个例子举例, 如果计算某函数的sum, 按照上述例子, 需要三个参数, $n$/$f$/$g$, 返回值是求某上限是$n$的$f$|$s$的和的值. 如果将函数作为返回值, 此处值需要两个参数, 返回值代表求某$f$|$g$的和的方法, 意义是不一样的.

修饰器等相当于是语言的语法糖, 这里不就记述了.

小结

什么时候用到高阶函数? 当我们在函数内部还能抽象出某些函数的时候, 就应该使用高阶函数了.

总结

  1. 注意中缀记号和函数调用的优缺点, 一个简洁, 一个扩展性高;
  2. 程序运行依赖于环境, 有全局环境和对每个函数的局部环境;
  3. 黑盒应该让用户用起来很自然, 没有任何意外的输入或输出;
  4. 当函数内部还能抽象出一些通用方法是, 应该考虑考虑高阶函数;
更新于 2021-08-10
CC BY-NC 4.0
 软件设计
 SICP, Python